|
|
|
|
 |
 |
 |
| |
 |
|
  
|
|
|
| |
|
|
| |
 Shape Index Shape Index |
 |
|
With some of the tests, it was important that the comparison of the user’s score profile and the score profiles of each of the careers be based on the shape or pattern of the scores, rather than the absolute level or amount of each score. For example, with the Interest Inventory test, there was no concern about directing a user to explore careers that were “under” or “over” a critical level of interest. Rather, it was more important to identify patterns of interests, rather than absolute levels. The goal was to direct users to occupations that tended to have the same high interests, as well as the same low interests – in other words, similarities in pattern or shape.
When a user provides a score profile from one of the tests, the correlation coefficient serves as the index of correspondence. The correlation between a client’s profile (X) and a career profile (Y) is given mathematically as follows:
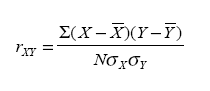
Where 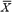 and and 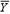 and and 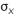 and and 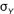 are the means and standard deviations of X and Y, respectively, and N is the number of scores to be correlated (i.e., the number of scores constituting the user’s profile). The correlation indexes the similarity of the shape (but not the level) between the client and occupation profiles and is the correspondence index most vocational counselors prefer. The correlation can range from -1.0 to +1.0. A correlation of +1.0 indicates that the rank orders of user and career scores are identical, whereas a correlation of -1.0 indicates that the rank order of a user’s score is opposite the rank order of a career score. A value of 0.0 indicates no correspondence between the user score profile and the career score profile. For simplicity in presentation and greater user comprehension, the correlation coefficient was transformed into a percentage between 0% and 100%. are the means and standard deviations of X and Y, respectively, and N is the number of scores to be correlated (i.e., the number of scores constituting the user’s profile). The correlation indexes the similarity of the shape (but not the level) between the client and occupation profiles and is the correspondence index most vocational counselors prefer. The correlation can range from -1.0 to +1.0. A correlation of +1.0 indicates that the rank orders of user and career scores are identical, whereas a correlation of -1.0 indicates that the rank order of a user’s score is opposite the rank order of a career score. A value of 0.0 indicates no correspondence between the user score profile and the career score profile. For simplicity in presentation and greater user comprehension, the correlation coefficient was transformed into a percentage between 0% and 100%. |
|
 |
|
 |
 |
 Distance Index Distance Index |
 |
|
When determining the correspondence between a client score profile and corresponding career score profiles where level is a relevant factor, the matching procedure needs to incorporate distance as well as shape in determining similarity. For example, in the Skills Profiler, the level of scores matters as much as the pattern, and therefore needs a second index to refine the profile correspondence. Here, a normalized Euclidean Distance algorithm was chosen to determine similarity.
The Euclidean distance between two measures X and Y is given mathematically as follows:

where X and Y are scores from the user and career profiles, respectively, and k is the number of scores in a given score profile. The d value indexes the proximity of the user profile to the career profile. Thus, Euclidean distance introduces level to the matching process. The matching program uses d in the matching algorithm for the Skills Profiler, for example, because the goal is to increase the face validity of the selected careers by guiding users to careers that not only correspond to the pattern of their skills, but for which they are also more likely to be qualified rather than under- or over-qualified.
|
|
 |
|
 |
 |
 Composite Scoring Composite Scoring |
 |
|
A correlation coefficient algorithm again served as the index of correspondence in development of a composite scoring system. The computation of the correlation, however, required a few extra steps.
To calculate the correspondence between a composite user profile and career score profiles appropriately, two factors had to be addressed. First, the scores on the various tests are all scaled differently. Due to differences in scaling, the composite correlations between user and career profiles would likely be skewed. For example, consider a hypothetical composite client profile comprising scores from the Interest Inventory (six scores, ranging from 0-25) and the Work Values Assessment test (twenty scores, ranging from 1-5). Without adjusting for differences in scale, the Work Values Assessment will naturally produce higher correlations and influence the composite score more than the Interest Inventory. Therefore, the scores for each test under consideration must be standardized within each measure before calculating the composite correspondence.
Second, because each test yields a different number of scores to the composite score profile, the correlation between a user profile and a career profile will primarily depend upon the measure that contributes more scores to the profile. Therefore, the composite algorithm needed to correct for differences in the number of questions as well scale.
The solution was found in counter-weighting and averaging correlations such that differences in the number of questions, as well as scale, were offset. A mean weighted correlation, however, is not a final index of correspondence. Whenever one averages correlations, one typically applies Fisher’s r to z transformation to each of the correlations before averaging, and the Fisher inverse transformation after:
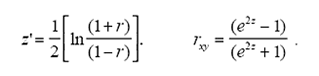
To summarize, the mean index of correspondence between a user’s composite score profile and a career’s total score profile was calculated by (a) determining the correlation between the user and career profiles for each test, (b) transforming each of those correlations to Fisher z values, (c) calculating the mean of the Fisher z values, and (d) transforming the mean z value back to the correlation metric.
|
|
 |
|
 |
 |
|
 |
|
|
| |
|
|
 |
|
 |
 |
 |
| |
|
|
| Interesting Fact |
 |
|
 |
| The U.S. industry expected to experience the greatest decline between 2002 and 2012 is Apparel Manufacturing. |
|
|
 |
| Did you know... |
 |
|
 |
| The MyPlan.com Career Assessment Tests provide more detailed career recommendations than any other set of tests available anywhere! |
|
|
|
|
 |
|
|